Home dimensiion reduce
Post
Cancel

dimensiion reduce

Posted Jun 15, 2023 Updated Jul 26, 2023
By Jialiang Chen
18 min read

这篇文章的介绍了我学习降维的一些知识，主要会包括以下Paper:

Here a reference list is provided. You need to read all the papers in the list and write a literature review about the above-mentioned methods.

  1. Kernel Principal Components Analysis
  2. A kernel view of the dimensionality reduction of manifolds
  3. A duality view of spectral methods for dimensionality reduction
  4. An Introduction to Nonlinear Dimensionality Reduction by Maximum Variance Unfolding
  5. A Global Geometric Framework for Nonlinear Dimensionality Reduction
  6. Nonlinear Dimensionality Reduction by Locally Linear Embedding
  7. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation
  8. Fisher discriminant analysis with kernels

A discussion on these methods is strongly encouraged based on your understanding. You may discuss on issues such as, for example, the underlying connections of these methods, pros/cons of each method (or anything that you think is interesting).

降维方法综述

数据降低维度旨在将高纬数据嵌入到低维空间，有助于下游任务（如分类、聚类等）的分析处理。

这篇文章总结了一些经典的降维方法，包括LDA、KLDA、PCA、KPCA、MDS、Isomap、LLE、Laplacian eigenmap、MVU等方法。在总结各个方法后，在不同纬度做了方法间的比较分析。

Notation: 这篇文章将原始数据维度记为 N，降低后的数据维度记为 K。

PCA

PCA(Principle Components Analysis) 主成分分析是一种线形的降维方法，它主要适用于无监督场景。主成分分析的想法主要是，通过线形变化，将原始数据中的变量结合成新的变量（Principle Components）这些成分相互独立（特征向量正交），在降低维度时则假设方差更大的成分更重要，保留方差较大的成分、舍弃方差小的成分。

PCA 主要过程

  1. 归一化数据 $X=X-mean(X)$
  2. 计算协方差矩阵 $Cov(X)=\frac{1}{N}\sum_{i=1}^{N}{x_i^Tx_i}$
  3. 通过 SVD 等方法计算协方差矩阵的特征值和特征向量 $C\mathbf{v} = \lambda\mathbf{v}$
  4. 选择前 K 大特征值对应的特征向量
  5. 根据特征向量获得主成分（降低维度后的数据）

KPCA

Kernel PCA的过程和 PCA 很类似，由于 PCA 的方法只能处理变量间的线性关系，但是真实数据往往是非线性的。所以引出了 Kernel PCA 方法。Kernel PCA 将 Kernel Trick 引入 PCA，从而使得 PCA 具有非线性的能力。核技巧的核心思想是将低维空间中的数据映射到一个高维特征空间，使得原始的非线性关系在高纬特征空间中变得线性可分。所以KPCA的思想主要是先将数据映射到高维空间，再使用PCA方法来获取主成分。

KPCA 主要过程

与PCA方法类似，KPCA方法主要过程如下：

  1. 使用核函数计算核矩阵，例如高斯核函数 $K(i,j) = exp(-gamma * x_i- x_j ^2)$

  2. 核矩阵中心化。$\mathbf{1_N}$代表N*N的矩阵，其每个元素都为 1/N

    \[K' = K - \mathbf{1_N} K - K \mathbf{1_N} + \mathbf{1_N} K \mathbf{1_N}\]

3-5. 和PCA方法中的 3-5 相同。

LDA

LDA(Linear Discriminant Analysis)，是一种线形的降维方法，需要有标签数据，适用于有监督学习场景。LDA假设同一类别的样本具有相似的分布，通过最小类内距离(由类内散度矩阵衡量 within-class scatter matrix, sw)，最大化类间距离(由类间散度矩阵来衡量 between-class scatter matrix, sb)找到将高维数据投影到低维的最佳投影方向，从而实现数据的降维。

LDA想要找到一个投影方向 $y = wx$，最大化 generalized Rayleigh quotient

\[J(w) = \frac{w^TS_bw}{w^TS_ww}\]

LDA（Linear Discriminant Analysis）的主要过程：

  1. 计算类别内散度矩阵（within-class scatter matrix）Sw：

    \[Sw = \sum_{k=1}^{K} \sum_{i=1}^{N_k} (x_i - m_k)(x_i - m_k)^T\]

    其中，xi是第i个样本的特征向量，mk是第k个类别中样本的均值特征向量。

  2. 计算类别间散度矩阵（between-class scatter matrix)，其中，m是整个数据集的均值特征向量。

    \[Sb = \sum_{k=1}^{K} N_k (m_k - m)(m_k - m)^T\]
  3. 计算 Sw的逆矩阵乘Sb矩阵的特征值和特征向量：$Sw^{-1} Sb \mathbf{v} = \lambda \mathbf{v}$
  4. 选择最大的k个特征值对应的特征向量，构成投影矩阵W。
  5. 使用投影矩阵W计算出投影后（降维后）的数据

LDA vs PCA

可以看到LDA 方法和 PCA 方法有很多相似之处，如都是数据降低维度的方法、都需要用到特征值分解，都有类似于协方差矩阵的出现（类内散度矩阵和协方差矩阵只相差了一个常数项）。但两者也有很多不同之处。LDA和PCA方法的 idea 或 motivation 不一样，PCA主要是为了选取方差最大的主成分，面向无监督场景。LDA 是为了最大类内距离、最小类间距离，面向有监督场景。

KLDA

Kernel LDA 的想法也是将 Kernel Metric 引入 LDA 方法。对于非线性数据，LDA并不适用。KLDA的主要想法是通过核函数，将数据映射到高维空间，转化为线性问题，在高维空间中再使用LDA。通过最大化类内散度和最小化类间散度，kLDA能够在低维空间中保留重要的判别信息。

MDS

MDS (Multidimensional scaling) 降维方法基于假设：在低维的空间中，数据的相对距离得到保持。这里的距离可以有不同的定义，如可度量的欧氏距离、曼哈顿距离等，对应于（metric MDS）也可以是不可度量的，如距离排序等，对应于 non-metric MDS。不同度量的选择也让MDS可以线性可以非线性，如使用欧氏距离是线性的。

MDS的方法主要流程：

  1. 根据度量距离函数计算两两点之间的距离，得到距离矩阵 $\mathbf{D} \in \mathbb{R}^{N \times N}$

  2. 构建双中心化距离矩阵  $\mathbf{B} \in \mathbb{R}^{N \times N}$ ，去除绝对尺度的影响，只保留样本之间的相对距离信息

    \[\mathbf{H} = \mathbf{I} - \frac{1}{N}\mathbf{1_{N}}\mathbf{1_{N}}^T \\ \mathbf{B} = -\frac{1}{2}\mathbf{HDH}\]

    其中，$\mathbf{I}$ 是 N 维的单位矩阵，$\mathbf{1}_{N}$是大小为 $N$ 的全1向量。

  3. 对 $\mathbf{B}$ 进行特征值分解得到特征值和特征向量
  4. 选择前 k 个最大的特征值和对应的特征向量
  5. 将原始坐标进行低维坐标映射，映射到 k 维中

MDS vs PCA

MDS 和 PCA 都是无监督算法，MDS和PCA方法的区别主要在于 Assumption，MDS 想保留相对距离，PCA方法则关注主成分方差。

Isomap

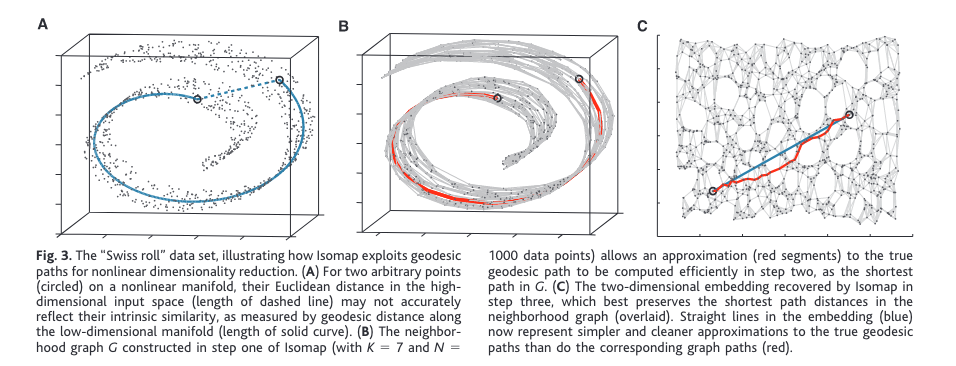
Isomap是一种非线性降维算法，它是从 MDS 方法发展而来的。 Isomap的核心思想是假设高维数据样本分布在一个低维流形上，利用数据样本之间的近邻关系构建一个图形结构，然后通过计算图形中节点之间的最短路径距离来近似测地距离 (geodesic distance)。然后使用这个测地距离来代表 MDS 的距离，后续操作和MDS相同。使用构建图结构后的最短距离，Isomap 保持降低维度后的数据测地距离相似，获得了非线性的能力，可以处理瑞士卷等流形数据（使用PCA 和 MDS 这些线性方法没有）。Isomap 算法继承了 PCA 和 MDS 方法的可迭代性，确保了多项式的时间复杂度。

截屏2023-07-01 21.18.52.png

Isomap 主要流程

  1. 构建临接图 G(V, E)。对于每个样本 i，选择其 k 个最近邻样本，得到近邻图G。
  2. 计算两两之间的最短路径，得到近邻图G中所有节点之间的最短路径距离矩阵D，图上最短距离的计算方法有：
    1. Dijkstra 算法
    2. Floyd-Warshall 算法
  3. 对于测地距离矩阵 D 输入到 MDS（Multidimensional Scaling）算法中，进行降维操作。

LLE

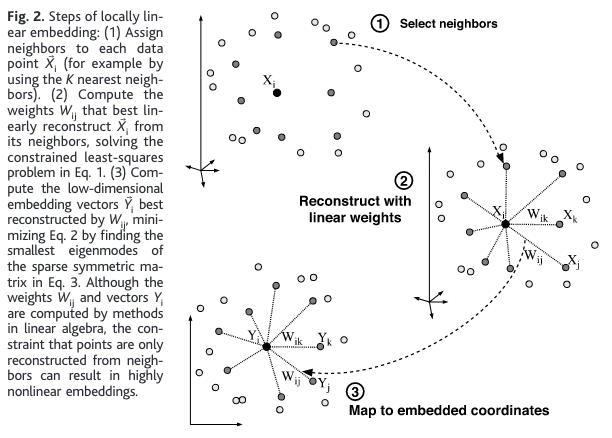
Local Linear Embedding 作为一种非线性流行学习的方法，他的思想是通过保持数据间的局部线性结构捕捉数据的局部关系，从而实现数据降维。对于每个数据点，都可以由与其相邻的数据点线性组合得到。

截屏2023-07-02 11.18.27.png

LLE 方法的主要流程

  1. 对于每一个数据点，选择 K 近邻

  2. 通过最小化 Cost 函数 （重构函数）计算出权重矩阵W

    \[W = \arg\min_{W} \sum_{i=1}^{n} \| x_i - \sum_{j=1}^{n} w_{ij} x_j \|^2\]

    其中 $\sum{w_{ij}} = 1$。这一步是一个约束最优化的问题，可以使用凸优化理论中的一些方法来求解，如拉格朗日乘子法。

  3. 确定降维后的维度 d, 最后的使用求得的权重矩阵 W 来最小化 Y( embedding cost function )
\[Y = \arg\min_{Y} \sum_{i=1 }^{n} \| y_i - \sum_{j=1}^{n} w_{ij} y_j \|^2\]

LLE vs Isomap

可以看到 Isomap 方法与 LLE 方法有很多相似之处，比如他们都是非线性的算法，克服了线形算法 PCA 、 LDA 的缺陷，他们都需要 K 近邻信息。但是他们的思想还是有许多不同之处，Isomap 论文较早，它更关注数据之间的全局结构，需要计算两两数据点之间的最短距离，所以计算复杂度较高。而LLE则更关注局部结构，只需要计算两个最优化问题，复杂度较低，更适合数据集较大的情况。

Laplacian eigenmaps

将拉普拉斯算子短思想引入到降维过程中。拉普拉斯算子 拉普拉斯算子在描述图的特征时，考虑了图的流形性质。它通过邻接关系和权重矩阵，将图的局部结构和全局结构综合起来，从而能够较好地保持图的流形性质。相比较 Isomap 等方法，只关注local信息，对噪声不敏感，算法的适用性更广。

算法流程

  1. 构建临接图
    • epsilon 理解 $x_i - x_j < \epsilon$，欧氏距离。优点：保留图结构，缺点：可能会将图分割成很多子图，且很难选择 $\epsilon$
    • k近邻 （优点：构造简单，图不会断，缺点，损失图结构信息）
  2. 计算权重，权重的选择有：
    • Heat Kernel $W(i, j) = \exp \left(-\frac{|x_i - x_j|^2}{\sigma^2}\right)$
    • $W_{ij} = 1$ if connected
  3. 根据权重矩阵W构建拉普拉斯矩阵  $L = D - W$, 对角线元素D(i, i)表示数据点 i 的度，即与 i 相连的边的权重之和。(然后 归一化 L， $L = I - D^{-1/2} \cdot W \cdot D^{-1/2}$， 消除了度的影响，使得在降维过程中更加关注数据点之间的相对距离和连接关系）
  4. 计算特征值和特征向量，选择前 k 个最小非零特征值对应的特征向量
  5. 映射得到降维表示

通过分析最优化函数，LLE 是 LE 的特例（近似）。

MVU

Maximum Variance Unfoldiing 展开将降维看成一种二次问题。这个方法的思想是在最大化降维后相邻点的距离的同时让降维后的数据点距离与原始数据距离相同（或最小化）。目标函数可以写为

\[J(P) = \frac{1}{2} \sum_{i,j} W_{ij} (||P^T x_i - P^T x_j||_2^2 - ||y_i - y_j||2^2)^2 - \lambda \sum{i} ||y_i - \bar{y}||_2^2\]

W是邻接图的权重矩阵 (临接图的构造和Isomap、LE 等方法类似) x_i和x_j是高维数据点，y_i\和(_j是它们在降维后的数据点，\lambda\是正则化参数。

求解方式：在“An Introduction to Nonlinear Dimensionality Reduction by Maximum Variance Unfolding” 论文中使用 SDP 方法求解 MVU 的目标函数。（没咋看懂）

优缺点分析

PCA & LDA 属于线形方法，线性方法有个共同的缺点是无法捕捉非线性结构（流形）。

PCA

  • 优点在于简单有效，能够捕捉数据中的主要方差方向，适用于线性相关的数据降维

LDA

  • 优点在于面向有监督的分类任务进行学习

MDS

  • 优点：能够保持数据的距离或相似度关系，适用于距离或相似度信息较为重要的降维问题。
  • 缺点是计算复杂度会较高

KPCA:

  • 优点：相较于PCA，可以对非线性数据进行降维
  • 缺点：计算复杂度高，需要进行参数调优

KLDA:

  • 优点：相较于LDA，可以对非线性数据进行降维
  • 缺点：计算复杂度高，需要进行参数调优，可能会出现过拟合的情况

Isomap：

  • 优点：类地距离关系来进行降维。它基于图论和流形假设，能够捕捉数据中的非线性结构
  • 缺点：对噪声较为敏感、计算复杂度高

LLE:

  • 优点：归结为稀疏矩阵特征值计算，计算复杂度相对较小
  • 缺点：需要进行参数调优，性能高度依赖于邻居数的选择

LE:

  • 优点：计算复杂度较小，该算法也可以用于聚类
  • 缺点：需要进行参数调优，不能有效保持数据全局结构

refs

  1. ChatGPT(turbo 3.5 version)
  2. https://en.wikipedia.org/wiki/Kernel_principal_component_analysis#:~:text=In the field of multivariate,a reproducing kernel Hilbert space.
  3. https://zhuanlan.zhihu.com/p/32658341
  4. https://en.wikipedia.org/wiki/Isomap
  5. https://en.wikipedia.org/wiki/Nonlinear_dimensionality_reduction
  6. Isomap paper: A Global Geometric Framework for Nonlinear Dimensionality Reduction 7.
Machine-Learning
machine-learning
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents

Adaboost

交叉熵 Cross Entropy

Comments powered by Disqus.