简介
深度学习中,优化理论起到至关重要的作用。对于有监督学习,一般会先定义一个损失函数,然后通过优化算法来尝试最小化损失函数,从而得到一个在训练集上拟合较好的模型。 虽然深度学习的模型往往是非凸的,但很多凸优化的算法,如梯度下降可以应用到模型训练过程中,在实践中能取得不错的结果。 在这篇综述/总结性质的文章中,我参考了现有的资料,总结归纳了目前深度学习中用到的优化算法(主要是Pytorch 库函数中的优化算法)。 我的出发点是希望通过这次的总结归纳,帮助自己更好的理解和使用优化算法。
优化方法总结
梯度下降算法
梯度下降方法(Gradient Descent, GD)是最基本的方法,也是所有算法的基石。算法思想是使用梯度信息迭代更新参数,来获得一个训练误差较小的模型。GD算法可以用数学公式表示如下:
\[\theta_{i+1} \leftarrow \theta_i - \alpha \nabla J(\theta_i)\]其中,$J(\theta)$是损失函数,$\theta$是待优化的参数向量。$\alpha$为学习率(learning rate),$\nabla J(\theta_i)$为损失函数在$\theta_i$处的梯度向量。
SGD
SGD(Stochastic Gradient Descent)[@bottou2010large]优化了梯度下降算法,SGD每次迭代时不是使用整个训练集计算梯度,而是随机选择一部分数据进行计算。在每一次迭代中,SGD会从训练集中随机选择一小批数据样本(称为mini-batch),计算这些样本的梯度,并根据梯度方向调整模型参数,使模型能够更好地拟合训练数据。相对于传统的梯度下降算法,SGD在处理大型数据集时更加高效,并且可以更快地收敛到局部最优解。 SGD的问题是训练过程中参数震荡,不太稳定。因此,在实际应用中,通常会结合一些技巧来提高SGD的性能,例如动量(Momentum)和自适应学习率(Adaptive Learning Rate)。
SGD 区别与 GD 的部分如下: \(\nabla J(\theta) = \frac{1}{n}\Sigma_{i=1}^{n} \nabla J(\theta_i)\)
SGD with momentum
SGD with momentum借用物理中动量的概念,结合历史的梯度信息和当前梯度信息来共同更新梯度计算,通俗来讲,在遇到梯度较小的点,可以借助之前的梯度信息,使函数不停留在鞍点[@sutskever2013momentum]。 下面公式中$\gamma$ 作为动量的衰减系数,$v_t$作为最后的梯度信息
\[v_{t} = \gamma v_{t-1} + \nabla J(\theta_{t}) \\ \theta_{t+1} \leftarrow \theta_t - \alpha * v_t\]另一种实现方式在动量项中不考虑学习率,略有不同:
\[v_{t} = \gamma v_{t-1} + \alpha \nabla J(\theta_{t}) \\ \theta_{t+1} \leftarrow \theta_t - v_t\]在一般使用 SGD 时,我们会加上 weight decay,在大多数情况下,weight decay的作用和不调整损失函数的L2正则方法相同。
我们使用$\lambda$代表weight decay 参数,最后的SGD公式如下:
\[g_t = \nabla J(\theta_{t}) + \lambda\theta_t \\ v_{t} = \gamma v_{t-1} + g_t \\ \theta_{t+1} \leftarrow \theta_t - \alpha v_t\]Nesterov Accelerated Gradient
NAG是对 Momentum 的改进,NAG 的思想是提前走一步,即使用 \(\hat{\theta_t} \leftarrow \theta_t - \alpha \gamma v_{t-1}\) 来代替原来的参数计算梯度。NAG算法相对于Momentum多了一个本次梯度相对上次梯度的变化量,这个变化量本质上是对目标函数二阶导的近似。由于利用了二阶导的信息,NAG算法才会比Momentum具有更快的收敛速度[@NAG-zhihu,sutskever2013momentum]。
完整的NAG算法如下:
\[g_t = \nabla J(\theta_t - \alpha \gamma v_{t-1}) + \lambda\theta_t \\ v_{t} = \gamma v_{t-1} + g_t \\ \theta_{t+1} \leftarrow \theta_t - \alpha v_t\]###自适应学习率的梯度下降方法 Adaptive gradient methods 之前提到的GD方法对每个参数都基于相同的学习率。从经验的角度看,很多深度学习的数据集都具有长尾分布。对于不常见的特征,与其相关的参数得到更新机会较少。随着训练过程,学习率会下降,常见特征的参数更新次数较多,可以较快地收敛到最佳值,但对于不常见的特征,收敛较慢,很难得到一个较好的值。 所以,自适应调整学习率的方法希望对于那些更新不频繁的参数,每次更新时单次步长更大,能够多学习到一些知识。而对于更新非常频繁的参数,采用较小的步长,从而能够学到更稳定的参数值。 这一类的方法有 Adagrad,Adadelta,Adam 等。
AdaGrad[@duchi2011adaptive]
AdaGrad 采用让学习率除以历史梯度的平方和的方式调整学习率。此外,随着训练过程推移,AdaGrad 算法最终会让学习率趋向于0,这可以防止训练的不稳定但也可能让模型限制在了局部最优,下面提到的 RMSPRrop 和 AdaDelta 算法的设计就是为了改进这一点。
下面展示了 AdaGrad 公式(加上weight decay):其中 $\epsilon$表示一个较小的常量,防止divide-by-zero错误。
\[g_t = \nabla J(\theta_{t}) + \lambda\theta_t \\ s_t = s_{t-1} + g_t^2 \\ \theta_{t+1} \leftarrow \theta_t - \frac{\alpha}{\sqrt{s_t + \epsilon} } g_t\]值得一提的是,在 Pytorch 的AdaGrad实现中,还额外实现了 lr decay 功能(独立于 lr scheduler)。
RMSprop
RMSprop 算法的思想是不累加所有的历史梯度,而只关注一段时间内的梯度,让时间久远的梯度信息呈指数衰减 (类似于动量的想法),从而防止累加的梯度过大,学习率过小。
下面展示了公式,可以看到和 AdaGrad 的区别就在于状态 $s_t$ 的计算过程,其中$\beta$代表了让$s_t$衰减的参数。
\[g_t = \nabla J(\theta_{t}) + \lambda\theta_t \\ s_t = \beta s_{t-1} + (1-\beta)g_t^2 \\ \theta_{t+1} \leftarrow \theta_t - \frac{\alpha}{\sqrt{s_t + \epsilon} } g_t\]AdaDelta[@zeiler2012adadelta]
在 AdaDelta 中,学习率的大小由 $\Delta x_t$ 的平均值决定,因此当 $\Delta x_t$ 变小时,学习率会相应地减小,从而避免跨越全局最优点。 由于 AdaDelta 不需要手动设置学习率,因此它的超参数相对来说比较少,更容易调整。
AdaDelta 的更新规则如下:
\[g_t = \nabla J(\theta_{t}) + \lambda\theta_t \\ s_t = \beta s_{t-1} + (1-\beta)g_t^2 \\ \Delta x_t = \frac{\sqrt{u_{t-1} + \epsilon}}{\sqrt{s_t + \epsilon}} g_t \\ u_t = \beta u_{t-1} + (1-\beta) \Delta x_t^2 \\ \theta_{t+1} \leftarrow \theta_t - \Delta x_t\]Adam[@kingma2017adam]
在实践中,Adam 算法通常表现出色,并且不需要手动调节超参数,因此被广泛应用于各种深度学习任务中。从原理上看,Adam 算法可以简单看成是 RMSprop + Momentum。 但是 Adam 的作者发现在训练刚开始时,梯度的均值方差接近于0(太小了),所以作者做了一些归一化的操作,随着训练时间延长,归一化操作的作用会越来越小。
Adam 公式如下所示,其中$m_t$ 表示指数衰减的均值,$v_t$ 表示方差(和RMSprop 完全一致),$\beta$ 一般取值为 (0.9, 0.999) 这么取值的原因是方差变化比均值更剧烈, $\epsilon$一般取值为1e-08:
\[g_t = \nabla J(\theta_{t}) + \lambda\theta_t \\ m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t \\ v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2 \\ \hat{m_t} = m_t / (1-\beta_1^{t}) \\ \hat{v_t} = v_t / (1-\beta_2^{t}) \\ \theta_{t+1} \leftarrow \theta_t - \frac{\alpha * \hat{m_t}}{\sqrt{\hat{v_t} + \epsilon} }\]Adamax[@kingma2017adam]
Adam的变体Adamax使用无穷范数代替二范数,避免计算存储梯度的二阶动量。这样可以减少算法的计算量,同时在处理稀疏数据时也更为稳定。
\[v_t = \beta_2^\infty v_{t-1} + (1-\theta_2^p)g_t^\infty \\ = max(\beta_2 \dot v_{t-1}, |g_t|)\]Adamax 公式如下所示:
\[g_t = \nable J(\theta_t) + \lambda \theta_t \\ m_t = \beta_1m_{t-1} + (1-\beta_1) g_t \\ v_t = max(\beta_2 \dot v_{t-1}, |g_t| + \epsilon) \\ \hat{m_t} = \frac{m_t}{1-\beta_1^t} \\ \theta_{t+1} \leftarrow \theta_{i} - \alpha \frac{\hat{m_t}}{v_t}\]NAdam[@dozat.2016]
Nadam 是将Nesterov momentum 的思想引入Adam中。不同之处在于将“提前看梯度”转变成了“提前看动量”。即将
\[\hat{m_t} = \frac{m_t}{1-\beta_1^t} \\ = \frac{\beta_1 m_{t-1} + (1-\beta_1) g_t}{1-\beta_1^t} \\ = \beta_1\hat{m_{t-1}} + \frac{(1-\beta_1) g_t}{1-\beta_1^t} \\\]引入到最后一步的更新过程中,用 $\hat{m_t}$ 代替 $\hat{m_{t-1}}$
\(\theta_{t+1} \leftarrow \theta_t - \frac{\alpha}{\sqrt{\hat{v_t} + \epsilon}} * (\beta_1\hat{m_{t}} + \frac{(1-\beta_1) g_t}{1-\beta_1^t}) \\\) 这里的实现与Pytorch 中略微不同。
AdamW[@loshchilov2019decoupled]
AdamW是Adam算法的一种变体,旨在解决Adam算法在优化权重衰减(weight decay)时的缺陷。Adam算法中的权重衰减是通过在更新中添加一个惩罚项来实现的,但是这种做法会影响Adam的一阶和二阶动量估计,从而影响模型的收敛速度和精度。AdamW算法通过在权重更新前将权重进行L2正则化,从而避免了这个问题[@AdamW-zhihu]。图\ref{fig:fig1}展示了AdamW 与 Adam 的不同之处。 从经验的角度,AdamW比Adam的收敛性更好,目前的大模型训练(如GPT等)大多是使用AdamW。 
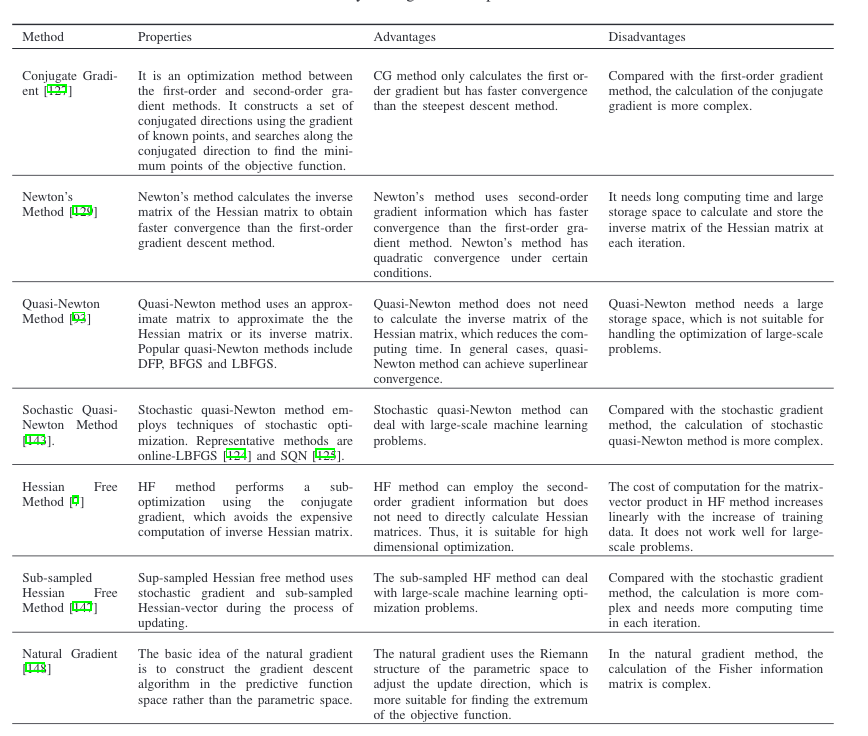
###其他方法 除了上述提到的较为常见的优化方法外,还有很多方法。如Prop、LBFGS、RAdam1、SVRG、ADMM、Frank-Wolfe等。 上面提到的方法都是一阶方法,没有使用二阶信息。二阶方法有 Conjugate Gradient、Newton’s Method、Quasi-Newton Method、 Hessian Free Method 等等。图~\ref{fig:table1}来自Sun~[@sun2019survey]等人的文章,详细总结了二阶/高阶方法。
refs:
On the Variance of the Adaptive Learning Rate and Beyond ↩

Comments powered by Disqus.